lattices package

The Lattice class

class lattices.Lattice(*, name=None, lattice_constants=None, nodal_positions=None, edge_adjacency=None, edge_coordinates=None, fundamental_edge_adjacency=None, fundamental_tesselation_vecs=None, **kwargs)

Bases: object

property UC_volume: float

Calculate unit cell volume from internally-stored crystal data

Given internally-stored crystal data \(a,b,c,{\alpha},{\beta},{\gamma}\), calculate unit cell volume as

\[abc \sqrt{1 - \cos({\alpha})^2 - \cos(\beta)^2 - \cos(\gamma)^2 + 2\cos(\alpha)\cos(\beta)\cos(\gamma)}\]

For more details see the supporting information of PNAS paper at https://www.pnas.org/doi/10.1073/pnas.2003504118

__init__(*, name=None, lattice_constants=None, nodal_positions=None, edge_adjacency=None, edge_coordinates=None, fundamental_edge_adjacency=None, fundamental_tesselation_vecs=None, **kwargs) → None

Construct lattice unit cell.

Takes in keyword-only arguments.

Examples

Three ways of initialisation:

• by specifying node coordinates and edge adjacency

>>> import numpy as np
>>> nodes = np.array([[0,0,0],[1,0,0],[0.5,1,0],[0.5,0.5,1]])
>>> edges = np.array([[0,1],[1,2],[0,2],[0,3],[1,3],[2,3]])
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges,
>>>               name='pyramid')
>>> lat
{'name': 'pyramid', 'num_nodes': 4, 'num_edges': 6}

• by specifying edge coordinates

>>> edge_coords = np.array([
>>>    [0,0,0,1,0,0],
>>>    [1,0,0,0.5,1,0],
>>>    [0.5,1,0,0,0,0],
>>>    [0,0,0,0.5,0.5,1],
>>>    [1,0,0,0.5,0.5,1],
>>>    [0.5,1,0,0.5,0.5,1]
>>> ])
>>> lat = Lattice(edge_coordinates=edge_coords, name='pyramid')
>>> lat
{'name': 'pyramid', 'num_nodes': 4, 'num_edges': 6}

• by specifying fundamental representation

>>> # simple cubic in fundamental representation
>>> nodes = [[0.5,0.5,0.5]]
>>> fundamental_edge_adjacency = [[0,0],[0,0],[0,0]]
>>> tess_vecs = [[0,0,0,1,0,0],[0,0,0,0,1,0],[0,0,0,0,0,1]]
>>> lat = Lattice(
>>>     nodal_positions=nodes,
>>>     fundamental_edge_adjacency=fundamental_edge_adjacency,
>>>     fundamental_tesselation_vecs=tess_vecs
>>> )
>>> lat.crop_unit_cell()
>>> lat
{'num_nodes': 7, 'num_edges': 6}

If both edge adjacency and fundamental edge adjacency are specified, simple checks are performed that the fundamental representation is consistent with the edge adjacency. In this case, lattice must be specified in a valid windowed configuration.

Lattice can also be initialised by directly unpacking the catalogue dictionary

>>> from data import Lattice, Catalogue
>>> cat = Catalogue.from_file('Unit_Cell_Catalog.txt', 1)
>>> lat = Lattice(**cat.get_unit_cell(cat.names[0]))
>>> lat
{'name': 'cub_Z06.0_E1', 'num_nodes': 8, 'num_edges': 12}

apply_nodal_imperfections(dr_mag: float, kind: str) → Lattice

Displace inner nodes using the fundamental representation.

Parameters:

• dr_mag (float) – magnitude of perturbation

• kind (str) – ‘sphere_surf’ or ‘sphere_solid’ or ‘gaussian’

Returns:

modified lattice with nodal imperfections

Return type:

Lattice

Examples

>>> nodes = [[0.3,0.3,0.5],[0.7,0.3,0.5],[0.3,0.7,0.5],[0.7,0.7,0.5]]
>>> fundamental_edge_adjacency=[[0,1],[1,3],[2,3],[0,2],[2,0],[3,1],[1,0],[3,2]]
>>> tess_vecs = [[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],
>>>              [0,0,0,0,1,0],[0,0,0,0,1,0],[0,0,0,1,0,0],[0,0,0,1,0,0]]
>>> lat = Lattice(
>>>     nodal_positions=nodes,
>>>     fundamental_edge_adjacency=fundamental_edge_adjacency,
>>>     fundamental_tesselation_vecs=tess_vecs
>>> )
>>> lat.crop_unit_cell()
>>> lat_imp = lat.apply_nodal_imperfections(0.1, 'sphere_surf')

(Source code, png, hires.png, pdf)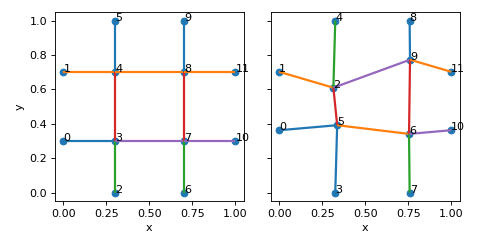

See also

calculate_fundamental_representation()

calculate_edge_lengths(edge_representation: str = 'cropped', coords: str = 'reduced') → ndarray[tuple[int, ...], dtype[_ScalarType_co]]

Calculate edge lengths in a given representation

Parameters:

• edge_representation (str, optional) – Use edges cropped to fit within unit cell window (‘cropped’) or fundamental edge representation (‘fundamental’). Defaults to ‘cropped’.

• coords (str, optional) – Use nodal coordinates in ‘reduced’ or ‘transformed’ coordinate system. Defaults to ‘reduced’.

Raises:

ValueError – if input parameters are not from the allowed set

Returns:

edge lengths of shape (num_edges,) if edge_representation`is ‘cropped’ or (num_fundamental_edges,) if `edge_representation is ‘fundamental’.

Return type:

np.ndarray

calculate_edge_radius(rel_dens: float, coords: str = 'transformed') → float

Calculate uniform edge radii according to relative density.

\[r = \sqrt{\frac{\bar{\rho} \ V}{\pi L}}\]

where \(\bar{\rho}\) is the relative density, \(V\) is volume of the unit cell, and \(L\) is sum of the edge lengths.

Parameters:

• rel_dens (float) – target relative density

• coords (str, optional) – Use ‘transformed’ or ‘reduced’ coordinates. Defaults to ‘transformed’.

Returns:

edge radius that gives the target relative density

Return type:

float

calculate_fundamental_representation() → None

Calculate the fundamental representation of lattice.

The fundamental representation is based on inner nodes and tesselation vectors.

Examples

>>> nodes = [[0,0.5,0.5],[1,0.5,0.5],[0.5,0,0.5],[0.5,1,0.5],[0.5,0.5,0.5]]
>>> edges = [[0,4],[1,4],[2,4],[3,4]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat.calculate_fundamental_representation()
>>> lat.node_types
{'corner_nodes': set(),
 'edge_nodes': set(),
 'face_nodes': {0, 1, 2, 3},
 'inner_nodes': {4}}
>>> lat.fundamental_edge_adjacency
[[4 4]
 [4 4]]
>>> lat.fundamental_tesselation_vecs
[[0. 0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 1. 0.]]
>>> lat.num_fundamental_edges
2

(Source code, png, hires.png, pdf)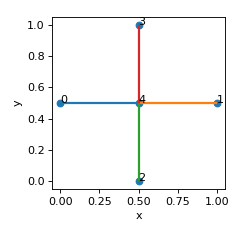

We see that this lattice has one inner node (4), and two fundamental edges:

• 4 –> 4 + [1 0 0] (horizontal edge connecting node 4 to its tesselation by vector (1,0,0))

• 4 –> 4 + [0 1 0] (vertical edge connecting node 4 to its tesselation by vector (0,1,0))

calculate_nodal_connectivity() → ndarray[tuple[int, ...], dtype[int64]]

Calculate how many times nodes appear in the edge adjacency map.

Returns:

connectivity of each node

Return type:

array[int] (num_nodes,)

calculate_node_distances(repr='reduced') → Tuple[ndarray, ndarray]

Calculate distances between all pairs of nodes.

Parameters:

repr – ‘reduced’ or ‘transformed’

Returns:

array of distances indices [num_pairs, 2]: indices of nodes corresponding to distances

Return type:

distances [num_pairs]

calculate_node_types() → Dict[str, Set]

Calculate types of nodes from reduced representation

Returns:

a dictionary with sets of

• corner_nodes (3 d.o.f. lie on UC boundary)

• edge_nodes (2 d.o.f. lie on UC boundary)

• face_nodes (1 d.o.f. lies on UC boundary)

• inner_nodes (no d.o.f lie on UC boundary)

Return type:

Dict[str, Set]

calculate_relative_density(coords: str = 'transformed') → float

Calculate relative density of the lattice.

Parameters:

coords (str, optional) – Use ‘transformed’ or ‘reduced’ coordinates. Defaults to ‘transformed’.

Returns:

relative density of the lattice

Return type:

float

check_window_conditions() → bool

Operate on reduced edge adjacency representation.

Check that

• minimum reduced node coordinate is 0 and maximum is UC_L (1)

• the only node types are face nodes and inner nodes

• the connectivity of these nodes is 1

• periodic partners come in pairs

See also

calculate_node_types(), calculate_nodal_connectivity(), check_periodic_partners()

collapse_nodes_onto_boundaries(tol=0.0001)

Collapse nodes which are close to boundaries onto the boundaries.

Operates on reduced nodal coordinates. All nodal coordinates which are very close to 0 or UC_L (within tolerance) will be replaced by 0 or UC_L, respectively.

create_tesselated(nx: int, ny: int, nz: int, merge_colinear=True) → Lattice

Create periodic tesselation of the lattice

Parameters:

• nx (int) – number of times to repeat in x-direction

• ny (int) – number of times to repeat in y-direction

• nz (int) – number of times to repeat in z-direction

Returns:

tesselated lattice

Return type:

Lattice

Examples

>>> nodes = [[0.2,0.3,0],[0.2,0,0],[1,0.3,0],[0.2,1,0],[0,0.3,0]]
>>> edges = [[0,1],[0,2],[0,3],[0,4]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lt = lat.create_tesselated(2,2,1)

(Source code, png, hires.png, pdf)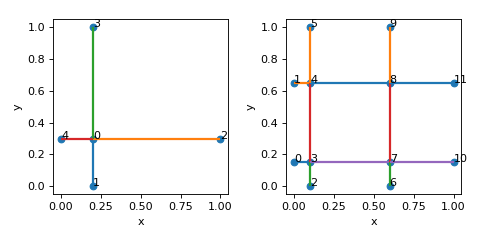

create_windowed(max_num_attempts: int = 10, min_edge_length: float = 0.005, return_attempts: bool = False) → Lattice

Create a windowed representation of a lattice

Returns:

a new lattice instance

Return type:

Lattice

Examples

>>> nodes = [[0,0,0],[1,0,0],[1,1,0],[0,1,0]]
>>> edges = [[0,1],[1,2],[2,3],[3,0]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat
{'num_nodes': 4, 'num_edges': 4}
>>> lat_w = lat.create_windowed()
>>> lat_w
{'num_nodes': 5, 'num_edges': 4}

(Source code, png, hires.png, pdf)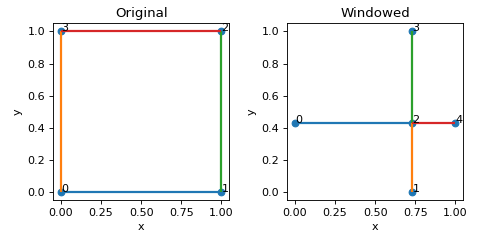

crop_unit_cell(reduced_edge_coords: ndarray[tuple[int, ...], dtype[_ScalarType_co]] | None = None) → None

Crop lattice to fit within unit cell window.

Examples

>>> nodes = [[0,0,0],[1.5,0.5,0]]
>>> edges = [[0,1]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat.crop_unit_cell()

(Source code, png, hires.png, pdf)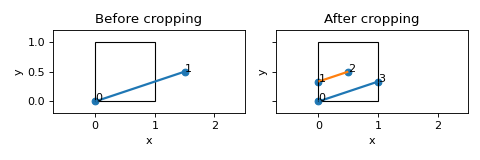

See also

create_windowed()

find_edge_intersections() → List[Tuple[Set, ndarray[tuple[int, ...], dtype[_ScalarType_co]]]]

Find intersections between edge pairs.

Operates on reduced adjacency representation.

Returns:

dictionary with edge indices

as keys and coordinates of intersection points as values

Return type:

edge_intersection_points

Example

>>> nodes = [[0,0,0],[1,0,0],[1,1,0],[0,1,0]]
>>> edges = [[0,2],[1,3]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat
{'num_nodes': 4, 'num_edges': 2}
>>> edge_intersections = lat.find_edge_intersections()
>>> print(edge_intersections)
[({0, 2}, array([[0.5, 0.5, 0. ]])), ({1, 3}, array([[0.5, 0.5, 0. ]]))]

(Source code, png, hires.png, pdf)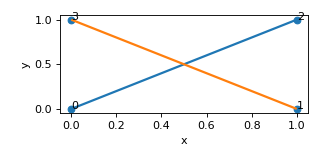

find_nodes_on_edges() → List[Tuple[Set, ndarray[tuple[int, ...], dtype[_ScalarType_co]]]]

Find nodes which lie on edges and are not endpoints.

Returns a list of tuples (edge: set, nodes: coordinates of points that need to split edges)

Example

>>> nodes = [[0,0,0],[1,0,0],[0.5,0,0]]
>>> edges = [[0,1]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat
{'num_nodes': 3, 'num_edges': 1}
>>> nodes_on_edges = lat.find_nodes_on_edges()
>>> print(nodes_on_edges)
[({0, 1}, array([[0.5, 0. , 0. ]]))]

(Source code, png, hires.png, pdf)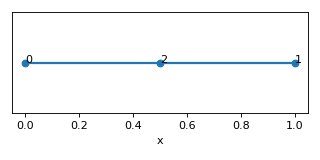

get_periodic_partners() → List[Set]

Calculate periodic partners.

Check is done first whether lattice is in a valid window condition.

Returns:

list of 2-element sets of node numbers of periodic partners

Return type:

list

Examples

Nodes {0,1} and {2,3} in the lattice below are periodic partners.

>>> nodes = [[0,0.5,0.5],[1,0.5,0.5],[0.5,0,0.5],[0.5,1,0.5],[0.5,0.5,0.5]]
>>> edges = [[0,4],[1,4],[2,4],[3,4]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat.get_periodic_partners()
[{0, 1}, {2, 3}]

(Source code, png, hires.png, pdf)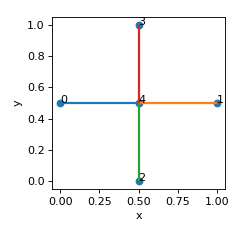

See also

check_window_conditions()

merge_colinear_edges() → None

Merge colinear edges based on nodal connectivity 2 and similar angle between two unit vectors along the edges.

Example

>>> nodes = [[0,0,0],[1,0,0],[0.5,0,0]]
>>> edges = [[0,2],[1,2]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat
{'num_nodes': 3, 'num_edges': 2}
>>> lat.merge_colinear_edges()
>>> lat
{'num_nodes': 2, 'num_edges': 1}

(Source code, png, hires.png, pdf)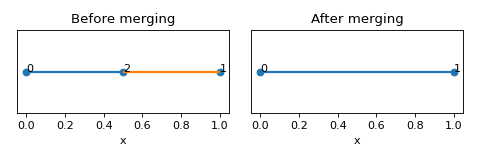

merge_nonunique_nodes(decimals: int | None = None) → None

Merge nodes with identical coordinates and collapse self-incident edges

obtain_shift_vector(max_num_attempts: int = 10, min_edge_length: float = 0.005, return_attempts: bool = False) → ndarray[tuple[int, ...], dtype[_ScalarType_co]]

Get a shift vector for windowed representation.

Raises:

• WindowingException – _description_

• WindowingException – _description_

Returns:

_description_

Return type:

npt.NDArray (3,)

refine_mesh(min_length: float, min_div: int) → Lattice

Split edges into at least ‘min_div’ segments per edge and with each segment having length at least ‘min_length’

remove_duplicate_edges_adjacency() → None

Remove duplicate edges.

Operates on the adjacency representation. Sort edges first

remove_duplicate_edges_nodes() → None

Remove edges which are on top of each other.

Operates on edge coordinate representation. To deal with machine precision, round all nodal coordinates to a specific number of decimal places.

remove_self_incident_edges() → None

Remove edges which have identical endpoints

Operates on the adjacency representation.

set_fundamental_edge_radii(edge_radii: Iterable | float) → None

Set radii of fundamental edges.

Parameters:

edge_radii (Union[Iterable, float]) – list of edge radii or single float

split_edges_by_points(edge_split_coords: List[Tuple[Set, ndarray[tuple[int, ...], dtype[_ScalarType_co]]]]) → None

Split edges at specific coordinate points.

Parameters:

edge_split_coords (List[Tuple[Set, npt.NDArray]]) – list of tuples (edge, point_array) in format as returned by functions find_nodes_on_edges() and find_edge_intersections(). Each edge will be split into multiple edges by the points in point_array.

Examples

>>> nodes = [[0,0,0],[1,0,0],[0.5,0,0]]
>>> edges = [[0,1]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat
{'num_nodes': 3, 'num_edges': 1}
>>> nodes_on_edges = lat.find_nodes_on_edges()
>>> lat.split_edges_by_points(nodes_on_edges)
>>> lat
{'num_nodes': 3, 'num_edges': 2}

(Source code, png, hires.png, pdf)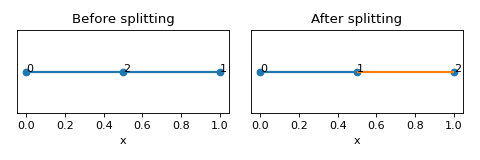

>>> nodes = [[0,0,0],[1,0,0],[1,1,0],[0,1,0]]
>>> edges = [[0,2],[1,3]]
>>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
>>> lat
{'num_nodes': 4, 'num_edges': 2}
>>> edge_intersections = lat.find_edge_intersections()
>>> lat.split_edges_by_points(edge_intersections)
>>> lat
{'num_nodes': 4, 'num_edges': 4}

(Source code, png, hires.png, pdf)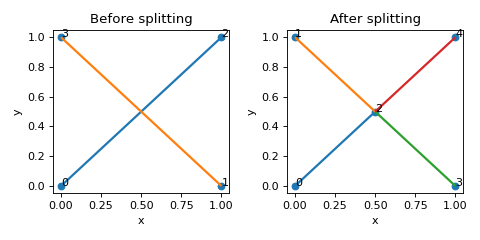

See also

find_nodes_on_edges() find_edge_intersections()

to_dict(fundamental: bool = True) → dict

Obtain a dictionary with the reduced representation.

transform_coordinates(coordinates: Iterable) → ndarray

Transform coordinates based on lattice constants.

Coordinates can be any O(3) vectors (e.g. node positions or edge vectors).

Parameters:

coordinates (Iterable) – broadcastable into shape (N,3)

Returns:

transformed coordinates

Return type:

np.ndarray (N,3)

property transform_matrix: ndarray[tuple[int, ...], dtype[float64]]

Assemble transformation matrix from crystal data.

Formula is in the Appendix to the PNAS paper: Lumpe, T. S. and Stankovic, T. (2020) https://www.pnas.org/doi/10.1073/pnas.2003504118.

update_representations(edge_coords: ndarray[tuple[int, ...], dtype[_ScalarType_co]] | None = None) → None

Propagate one format of representation to all other available formats.

Implemented options for basis: - ‘reduced_edge_coords’

# TODO: update all relevant attributes

property windowed_edge_radii: ndarray[tuple[int, ...], dtype[_ScalarType_co]]

Calculate edge radii for windowed edges from fundamental edge radii

Returns:

edge radii for windowed edges

Return type:

npt.NDArray

The Catalogue class

class data.Catalogue(data: dict, indexing: int, **attrs)

Bases: object

Unit cell catalogue object.

Note

Two class methods are available to initialise the object:

• from_file()

  Used to read the catalogue from a file

  >>> cat = Catalogue.from_file('Unit_Cell_Catalog.txt', 1)
  

• from_dict()

  Used to create the catalogue from unit cells either from scratch or when unit cells from a file are modified

  >>> nodes = [[0,0,0],[1,0,0],[0.5,1,0],[0.5,1,1]]
  >>> edges = [[0,1],[1,2],[0,2],[0,3],[1,3],[2,3]]
  >>> lat = Lattice(nodal_positions=nodes, edge_adjacency=edges)
  >>> lat
  {'num_nodes': 4, 'num_edges': 6}
  >>> cat_dict = {'pyramid':lat.to_dict()}
  >>> cat = Catalogue.from_dict(cat_dict)
  

  See Also:

  Lattice.to_dict()

classmethod from_dict(lattice_dicts: Dict[str, Dict]) → Catalogue

Generate unit cell catalogue from dictionary representation

Parameters:

lattice_dicts (Dict[str, Dict]) – dictionary of lattice dictionaries

Returns:

Catalogue

Note

Lattice dictionaries must contain the following keys:

• edge_adjacency

• nodal_positions or reduced_node_coordinates

They can contain also:

• lattice_constants

• compliance_tensors # assuming Voigt notation, legacy support

• compliance_tensors_V # Voigt notation

• compliance_tensors_M # Mandel notation

• fundamental_edge_adjacency

• fundamental_tesselation_vecs

• fundamental_edge_radii

• base_name

• imperfection_kind

• imperfection_level

• nodal_hash

classmethod from_file(fn: str, indexing: int, progress: bool = False, regex: str = None) → Catalogue

Read catalogue from a file.

Parameters:

• fn (str) – path to input file

• indexing (int) – 0 or 1 as the basis of edge indexing

• progress (bool, optional) – whether to show progress bar. Defaults to False.

• regex (str, optional) – regular expression to filter names. Defaults to None.

Returns:

Catalogue

classmethod get_names(fn: str) → List[str]

Retrieve names from catalogue without reading it into memory.

Parameters:

fn (str) – path to input file

Returns:

list of names

Return type:

List[str]

get_unit_cell(name: str) → dict

Return a dictionary which represents unit cell.

Parameters:

name (str) – Name of the unit cell from the catalogue that will be returned

Returns:

Dictionary describing the unit cell

Return type:

dict

Note

Returned dictionary contains all available keys from the following:

• name

• lattice constants: [a,b,c,alpha,beta,gamma]

• average connectivity

• compliance_tensors_M: dictionary {rel_dens: compliance tensor}

• compliance_tensors_V: dictionary {rel_dens: compliance tensor}

• nodal_positions: nested list of shape (num_nodes, 3)

• edge_adjacency: nested list of shape (num_edges, 2) (0-indexed)

• fundamental_edge_adjacency: nested list of shape (num_fundamental_edges, 2) (0-indexed)

• fundamental_tesselation_vecs: nested list of shape (num_fundamental_edges, 6) or (num_fundamental_edges, 3) (0-indexed)

• fundamental_edge_radii: dictionary {rel_dens: list of edge radii}

The dictionary can be unpacked in the creation of a Lattice object

>>> from data import Lattice, Catalogue
>>> cat = Catalogue.from_file('Unit_Cell_Catalog.txt', 1)
>>> lat = Lattice(**cat.get_unit_cell(cat.names[0]))
>>> lat
{'name': 'cub_Z06.0_E1', 'num_nodes': 8, 'num_edges': 12}

See also

data.Lattice.__init__()

static n_2_bn(name: str) → str

Convert name of a unit cell to base name.

Relies on the following naming convention:

[base_name]_p_[imperfection_level]_[nodal_hash]

where base_name is of the form:

[symmetry]_[connectivity]_[code]

For instance:

cub_Z12.0_E19_p_0.0_9113732828474860344

Parameters:

name (str) – Name of the unit cell

Returns:

Base name of the unit cell

Return type:

str

to_file(fn: str) → None

Export unit cell catalogue to file.

Parameters:

fn (str) – output file path